多重信号子空间分类算法

多重信号子空间分类算法通常又被称为多重信号特征法，这种信号子空间方法具有多信号同时测向能力，并且其方位分辨率较高，它的主要思想是：将阵列输出数据进行自相关处理后获得的协方差矩阵进行特征分解，得到信号子空间和噪声子空间，然后利用这两个子空间的正交性来构造MUSIC方位谱，此时方位谱的谱峰就是需要估计的信号方位。

本文主要记录MUSIC算法的相关推导以及相关因数对算法性能趋势的影响和仿真。

假设信号与噪声之间不具有相关性，同时各个阵元之间的噪声互相不相关，则根据窄带信号模型，其协方差矩阵为：

$$R = E[X { X^H } ] = AE[S { S^H } ] { A^H } + E[N { N^H } ] = A { R_s } { A^H } + { \sigma ^2 } I$$

其中，符号H表示矩阵的共轭转置。$S$表示目标信号，对$R$进行特征分解，则信号协方差矩阵可以由特征值和对应的特征向量表示为如下形式：

$$R { \rm { = } } \sum\limits_ { i = 1 } ^M { { \lambda _i } } { e_i } e_i^H$$

假设有$d(d < M)$个信号由远处入射到阵列，且认为这些信号都能被检测到，将获得的特征值由大到小排列后，可以划分协方差矩阵$R$特征分解后的特征值与特征向量：

$$\Lambda=\left[\begin{array}{cc}\Lambda_{S} & 0 \\ 0 & \Lambda_{N}\end{array}\right]$$ $$E=\left[\begin{array}{ll}E_{C S} & E_{C N}\end{array}\right]$$

式中，${\Lambda _S}$和${\Lambda _N}$分别是通过降序排列的信号特征值和噪声特征值构成的对角矩阵，${E_S}$和${E_N}$分别是由信号特征向量和噪声特征向量张成的信号子空间以及噪声子空间。由${E_S}$张成的空间，属于$A(\theta )$张成的空间的子空间，即

$$\operatorname{span}\left\{E_{S}\right\} \subseteq \operatorname{span}\{A(\theta)\}$$

式中，$span\{ {E_S}\} $表示由${E_S}$的列生成的子空间。如果入射到阵列的信号互相不相干，则信号协方差矩阵属于满秩矩阵，那么信号子空间中向量的个数等于这个空间的维数，所以存在如下关系：

$$\operatorname{span}\left\{E_{S}\right\}=\operatorname{span}\{A(\theta)\}$$ $$\operatorname{span}\left\{E_{N}\right\} \perp \operatorname{span}\{A(\theta)\}$$

由此，我们可以构造基于多重信号特征法的空间方位谱。因为扫描向量$a(\theta )$属于阵列流形向量空间和信号子空间，所以它与噪声子空间也存在正交关系，即有：

$$E_{N}^{H} a_{i}(\theta)=0, \quad i=1, \cdots d$$

所以扫描向量与$a(\theta )$噪声子空间的欧几里得距离(Euclidean Distance)的平方为:

$$\|l\|^{2}=a^{H}(\theta) E_{N} E_{N}^{H} a(\theta)=0$$

但是在实际情况中，通常无法与理想情况做到一致，如由于实际数据中噪声的影响，上式并不成立，因此，实际进行目标方位估计是通过最小化搜索的方式实现的，即：

$$\theta_{MUSIC}=\arg _{\theta} \min a^{H}(\theta) E_{N} E_{N}^{H} a(\theta)$$

所以，基于MUSIC算法的方位谱估计为

$$P_{MUSIC}=\frac{a^{H}(\theta) a(\theta)}{a^{H}(\theta) E_{N} E_{N}^{H} a(\theta)}$$

本部分通过仿真讨论在不同信号参数对MUSIC算法性能的影响，主要考虑当阵元数、阵元间隔、快拍数以及信噪比四个方面发生变化时进行仿真分析。假设3个非相干窄带信号入射到均匀线列阵，信号频率为2kHz，信号的入射角度分别为${10^ \circ }$、${30^ \circ }$、${50^ \circ }$，当阵元数、阵列孔径、快拍数以及信噪比变化时进行仿真分析。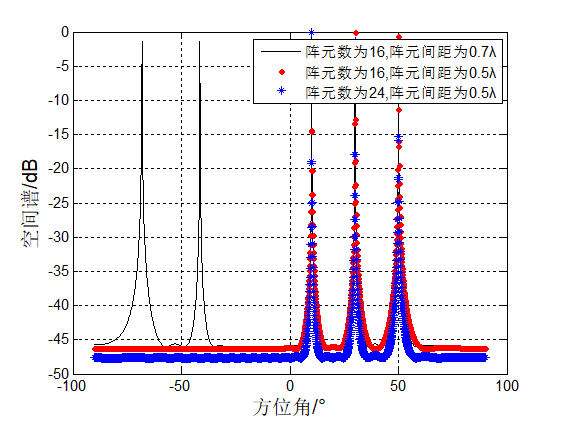

阵元数及阵列孔径发生变化对MUSIC算法性能曲线

分析阵元数以及阵列孔径对MUSIC算法影响时，分别采用16元阵和24元阵，阵元间隔分别为$0.5\lambda$和$0.7\lambda$，其中 为阵列接收信号的波长。仿真结果如上图所示。
由图可以看出，无论是改变阵元的数量或者改变阵列孔径的大小对MUSIC算法的性能均会产生影响：当阵元间距相同时，接收阵元数相对较多的信号空间谱，其谱峰明显尖锐，分辨率较高，当阵元数相同，阵元间距为$0.7\lambda$时，相对于阵元间距为$0.5\lambda$的空间谱，其估计性能明显下降，同时在$ - {68^ \circ }$和$ - {42^ \circ }$出现虚假谱峰，严重影响对目标方位的正确估计。
在分析快拍数和信噪比对MUSIC算法影响时，分别采用快拍数为1024和2048，信噪比为5dB和15dB的参数情况。仿真结果如图所示：

快拍数与信噪比发生变化对MUSIC算法性能曲线

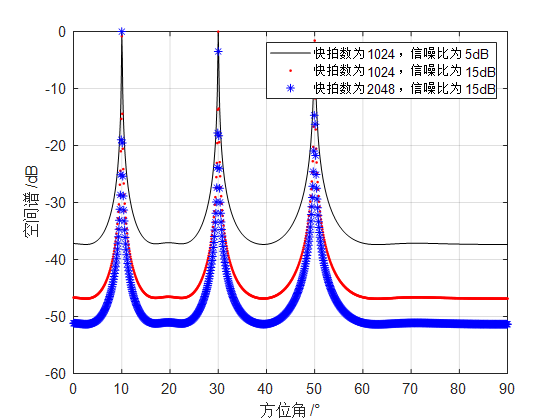
从上图中可以看出，信噪比和快拍数对MUSIC算法的方位估计效果均有显著影响，当信噪比均为15dB时，算法对快拍数较多的信号处理效果更好，当快拍数均为1024，信噪比分别为5dB和15dB时，MUSIC算法对15dB的信号估计效果明显优于5dB信号，其峰更加尖锐。

信噪比不同时MUSIC算法有效估计概率曲线

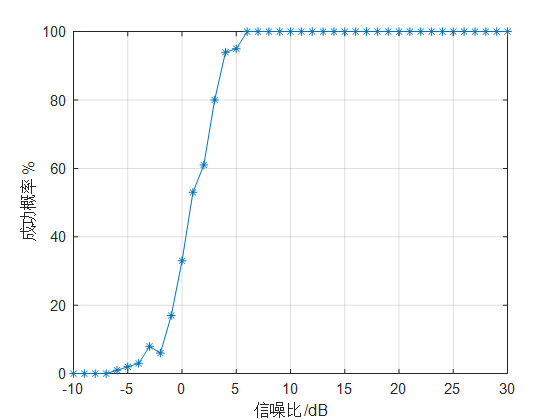
如上图所示，仿真是在其他条件保持不变的情况下，信号信噪比由-10dB提升至30dB，每提升1dB，以MUSIC算法独立重复进行100次方位估计实验，如果估计的角度与期望方位相差小于${1^ \circ }$，则认为估计有效，否则估计无效。当信噪比在0dB以下时，有效概率不足30%，基本无法正常工作，但是从-2dB至6dB之间，随着信噪比的增加，有效概率明显提升，信噪比大于6dB时完全可以正确估计目标。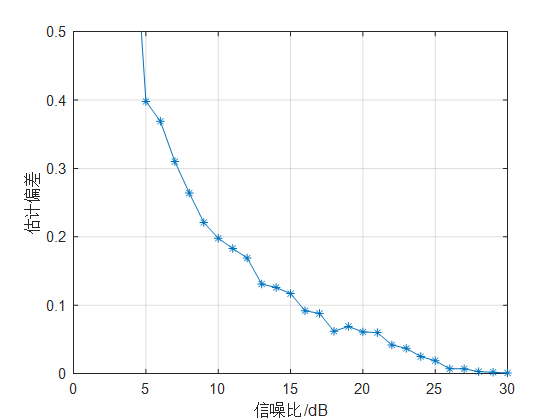

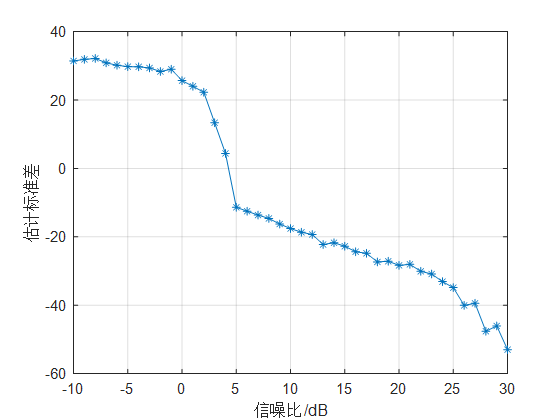
不同信噪比估计偏差曲线

不同信噪比估计标准差曲线
如以上两图所示，在上述条件下，对不同信噪比下的估计标准差以及估计偏差进行仿真。其中估计偏差为100次估计的方位偏离期望方位的平均值，估计标准差为对三个信号的估计偏差求平均标准差，随着信噪比提高，其估计偏差越来越小、并且出现估计偏差的概率会明显降低。

参考文献

1. 王永良. 空间谱估计理论与算法[M]. 清华大学出版社, 2004.