最小二乘滤波算法的基本算法是递归最小二乘算法,这种算法实际上是FIR维纳滤波器的一种时间递归实现,它是严格以最小二乘准则为依据的算法。它的主要优点是收敛速度快,所以在快速信道均衡、实时系统辨识和时间序列分析中得到了广泛应用。其主要缺点是每次迭代需要的运算量很大。

RLS原理

问题描述

考虑指数加权的优化问题：

$\min J_{n}(\boldsymbol{w})=\sum_{i=0}^{n} \lambda^{n-i}|e(i)|^{2}=\sum_{i=0}^{n} \lambda^{n-i}\left|y(i)-\boldsymbol{w}^{\mathrm{H}}(n) \boldsymbol{x}(i)\right|^{2}$

$0<\lambda \leq 1$为遗忘因子，这里只讨论平稳情况，取$\lambda=1$

$\begin{aligned} \frac{\partial J_{n}(\boldsymbol{w})}{\partial \boldsymbol{w}^{*}(n)}=& \frac{\partial}{\partial \boldsymbol{w}^{*}(n)} \sum_{i=1}^{n} \lambda^{n-i}\left[y(i)-\boldsymbol{w}^{\mathrm{H}}(n) \boldsymbol{x}(i)\right] \\ & \times\left[y(i)-\boldsymbol{w}^{\mathrm{H}}(n) \boldsymbol{x}(i)\right]^{*} \\ =& \boldsymbol{R}(n) \boldsymbol{w}(n)-\boldsymbol{r}(n) \end{aligned}$

从而得到最优解：

$\boldsymbol{w}_{\mathrm{opt}}(n)=\boldsymbol{R}^{-1}(n) \boldsymbol{r}(n)$

其中：

$\boldsymbol{R}(n)=\sum_{i=0}^{n} \lambda^{n-i} \boldsymbol{x}(i) \boldsymbol{x}^{\mathrm{H}}(i), \quad \boldsymbol{r}(n)=\sum_{i=0}^{n} \lambda^{n-i} \boldsymbol{x}(i) y^{*}(i)$

可以看到，$\lambda=1$对应的就是最小二乘思想。回头看看之前分析的LMS以及NLMS，用的是随机梯度下降的思想，这是RLS与LMS很明显的不同点。
由于$x(i)$、$y(i)$时刻在变换，最优解如何更新呢？

迭代更新

矩阵求逆引理：
设A和B是两个M*M正定阵，它们之间的关系为：

$\mathbf{A}=\mathbf{B}^{-1}+\mathbf{C D}^{-1} \mathbf{C}^{H}$

其中，D是NM正定阵，C是MN矩阵。根据矩阵求逆引理，可将A的逆矩阵表示为：

$\mathbf{A}^{-1}=\mathbf{B}-\mathbf{B C}\left(\mathbf{D}+\mathbf{C}^{H} \mathbf{B C}\right)^{-1} \mathbf{C}^{H} \mathbf{B}$

定义逆矩阵：

$\boldsymbol{P}(n)=\boldsymbol{R}^{-1}(n)$

利用逆阵求逆引理：

$\begin{aligned} \boldsymbol{P}(n) &=\frac{1}{\lambda}\left[\boldsymbol{P}(n-1)-\frac{\boldsymbol{P}(n-1) \boldsymbol{x}(n) \boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1)}{\lambda+\boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1) \boldsymbol{x}(n)}\right] \\ &=\frac{1}{\lambda}\left[\boldsymbol{P}(n-1)-k(n) \boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1)\right] \end{aligned}$

其中$k(n)$称为增益向量，由上式得出：

$\boldsymbol{k}(n)=\frac{\boldsymbol{P}(n-1) \boldsymbol{x}(n)}{\lambda+\boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1) \boldsymbol{x}(n)}$

借助迭代：

$\boldsymbol{R}(n)=\lambda \boldsymbol{R}(n-1)+\boldsymbol{x}(n) \boldsymbol{x}^{\mathrm{H}}(n)$ $\boldsymbol{r}(n)=\lambda \boldsymbol{r}(n-1)+\boldsymbol{x}(n) y^{*}(n)$

可以得到权重的更新公式：

$\boldsymbol{w}(n)=\boldsymbol{w}(n-1)+\boldsymbol{k}(n) \varepsilon^{*}(n)$

其中$\varepsilon(n)$为估计误差：

$\epsilon(n)=y(n)-\boldsymbol{w}^{\mathrm{H}}(n-1) \boldsymbol{x}(n)$

至此实现RLS的整个步骤。

RLS应用实例

算法步骤

结合上文的推导，给出RLS的迭代步骤：

初始化 $\boldsymbol{w}(0)=\mathbf{0}, \boldsymbol{P}(0)=\delta^{-1} \boldsymbol{I} \quad(0<\delta \ll 1)$ 其中$\delta$为很小的正数，如1e-7；
迭代更新 $\begin{array}{l} \varepsilon(n)=y(n)-\boldsymbol{w}^{\mathrm{H}}(n-1) \boldsymbol{x}(n) \\ \boldsymbol{k}(n)=\frac{\boldsymbol{P}(n-1) \boldsymbol{x}(n)}{\lambda+\boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1) \boldsymbol{x}(n)} \\ \boldsymbol{P}(n)=\frac{1}{\lambda}\left[\boldsymbol{P}(n-1)-\boldsymbol{k}(n) \boldsymbol{x}^{\mathrm{H}}(n) \boldsymbol{P}(n-1)\right] \\ \boldsymbol{w}(n)=\boldsymbol{w}(n-1)+\boldsymbol{k}(n) \varepsilon^{*}(n) \end{array}$

代码应用

function [e,w]=rls(lambda,M,u,d,delta)
% recursive least squares,rls.
w=zeros(M,1);
P=eye(M)/delta;
u=u(:);
d=d(:);
% input signal length
N=length(u);
% error vector
e=d.';
% Step2: Loop, RLS
for n=M:N
    uvec=u(n:-1:n-M+1);
    e(n)=d(n)-w'*uvec;
    k=lambda^(-1)*P*uvec/(1+lambda^(-1)*uvec'*P*uvec);
    P=lambda^(-1)*P-lambda^(-1)*k*uvec'*P;
    w=w+k*conj(e(n));
end

应用：

[s, fs, bits] = wavread(filename);         
s=s-mean(s);                          
s=s/max(abs(s));                      
N=length(s);                           
time=(0:N-1)/fs;                      
clean=s';
ref_noise=.1*randn(1,length(s));
mixed = clean+ref_noise;
mu=0.05;M=2;espon=1e-4;
% [en,wn,yn]=lmsFunc(mu,M,ref_noise,mixed);
% [en,wn,yn]=nlmsFunc(mu,M,ref_noise,mixed,espon);
delta = 1e-7;
lambda = 1;
[en,w]=rls(lambda,M,ref_noise,mixed,delta);

对应结果图：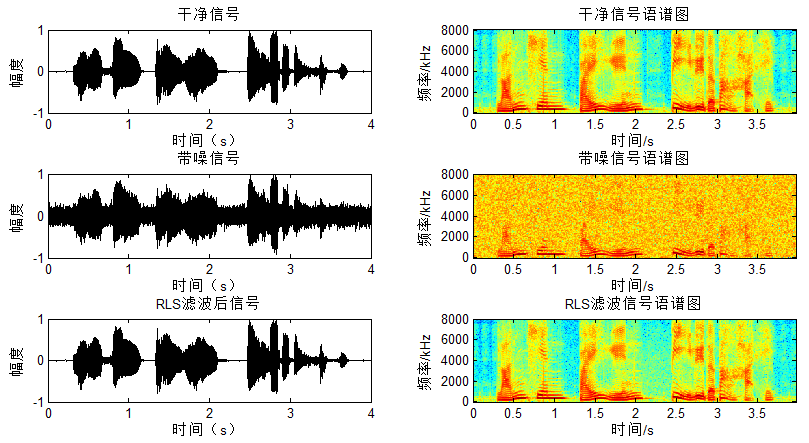

可以看出不像NLMS/LMS有一个慢速收敛的过程，RLS在开始阶段就得到较好的降噪。

对比LMS

与LMS对比，可以观察到RLS的几点特性：

平稳环境λ=1，其实是最小二乘的思想；LMS/NLMS是随机梯度下降思想；
最小二乘是直接得出结果，随机梯度下降收敛慢，因此RLS比LMS/NLMS收敛快一个数量级；