二阶锥规划(Second Order Cone Programming,SOCP)是凸优化问题的一个子集,通过引入二阶锥规划方法,可以解决大量优化设计问题,同时应用此方法,能解决方位估计算法包括旁瓣级、主瓣宽度、阵增益、稳健性在内的很多性能指标无法兼顾的问题,本部分介绍二阶锥规划优化设计方法,用于基于不同设计准则的空域矩阵滤波器求最优解。
对于一个向量空间$V$与它的一个子集 ,如果子集$C$中的任意一点$x$与任意整数$a$,其乘积$ax$仍然属于子集$C$,则称$C$为一个锥。若一个锥$C$中任意两点$x$与$y$,以及任意两个正数$a$与$b$,都有$ax + by$属于$C$,则该锥为凸锥。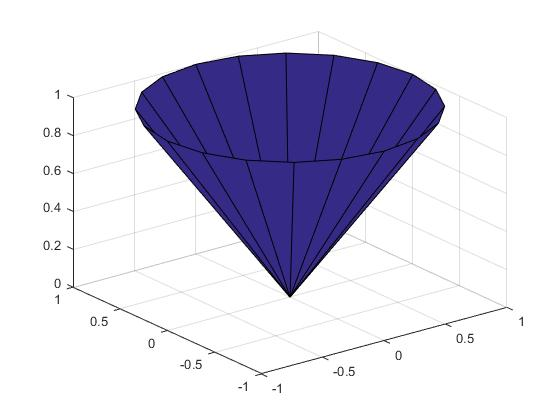
二阶锥规划是凸优化问题的一个子问题,它是在二阶锥约束和线性等式约束的条件下,最小化某线性目标函数,这是一种非常高效的求解算法,目的就是在满足约束条件的锥内寻找能够使目标函数最小化的最优点。其中二阶是指锥里面用到的是二范数,下式是一个二阶锥的表达式: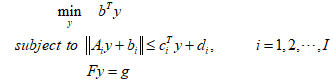
其中$b \in {C^{a \times 1}}$,$y \in {C^{a \times 1}}$,${A_i} \in {C^{({a_i} - 1) \times a}}$,${b_i} \in {C^{({a_i} - 1) \times 1}}$,${c_i} \in {C^{a \times 1}}$,$c_i^Ty \in R$,${d_i} \in R$,$F \in {C^{g \times a}}$,$g \in {C^{g \times 1}}$,每个不等式约束可以表示为如下二阶锥:
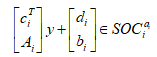
其中$SOC_i^ { { a_i } }$是空间${ C^ { { a_i } } }$的二阶锥,定义为
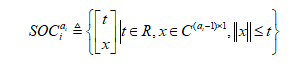
式中等式约束可以表示为
其中零锥${\{ 0\} ^g}$,定义为:
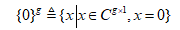
线性规划和凸二次规划都属于二阶锥规划,同时,由于二阶锥规划约束可以表示为线性矩阵不等式,所以它也是半定规划的子集。
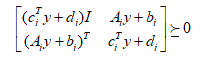
其中$I$表示单位矩阵
可以通过内点法求解二阶锥规划问题,例如SeDuMi,相比于半正定规划求解,通过这种方法求解此类优化问题速度更快。
参考文献
- Nesterov. Introductory Lectures on Convex Optimization: A Basic Course