正态/拉普拉斯/对数高斯/瑞利 分布

本文主要介绍正态分布、拉普拉斯分布等常用分布拟合的理论推导以及代码实现。

理论推导

假设数据独立同分布。对于任意数据点${x_i}$，对应概率密度为$f({x_i})$，最大似然函数：

$$J=\prod_{i=1}^{N} f\left(x_{i}\right)$$

表示成参数，并写成对数形式：

$$L(\theta)=\ln J(\theta)=\sum_{i=1}^{N} f\left(x_{i} ; \theta\right)$$

正态分布

对于正态分布：

$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$$

求偏导得参数估计：

$$\hat{\mu}=\frac{\sum_{i=1}^{N} x_{i}}{N}$$ $$\hat{\sigma}^{2}=\frac{\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}}{N}=\frac{(\mathrm{x}-\mu)^{T}(\mathrm{x}-\mu)}{N}$$

拉普拉斯分布

对于拉普拉斯分布:

$$f(x)=\frac{1}{2 b} e^{-\frac{|x-\mu|}{b}}$$

由于其概率密度曲线为对称分布，因此均值估计可用统计均值直接表示：

$$\hat{\mu}=\frac{\sum_{i=1}^{N} x_{i}}{N}$$

最大似然函数求偏导，得出b的估计：

$$\hat{b}=\frac{\sum_{i=1}^{N}\left|x_{i}-\mu\right|}{N}$$

对数正态分布

对数正态分布：

$$f(x)=\frac{1}{x \sqrt{2 \pi} \sigma} e^{-\frac{(\ln x-\mu)^{2}}{2 \sigma^{2}}}$$

事实上，令$t = \ln x$，则参数求解与正态分布完全一致。

$$\hat{\mu}=\frac{\sum_{i=1}^{N} t_{i}}{N}$$ $$\hat{\sigma}^{2}=\frac{\sum_{i=1}^{N}\left(t_{i}-\mu\right)^{2}}{N}=\frac{(\mathfrak{t}-\mu)^{T}(\mathfrak{t}-\mu)}{N}$$

瑞利分布

瑞利分布：

$$f(x)=\frac{x}{\sigma^{2}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$$

最大似然求导，得出参数估计：

$$\hat{\sigma}^{2}=\frac{\sum_{i=1}^{N} x_{i}^{2}}{2 N}$$

代码实现

正态分布

x       = x(:);                 % should be column vectors !
N       = length(x);
u       = sum(x)/N;
sig2    = (x-u)'*(x-u)/N;

拉普拉斯分布

x       = x(:);                 % should be column vectors !
N       = length(x);
u       = sum( x )/N;
b       = sum(abs(x-u))/N;

对数正态分布

t     = log(x(:));                 % should be column vectors !
N       = length(x);
m       = sum( t )/N;
sig2      = (t-m)'*(t-m)/N;

瑞利分布

x       = real(x(:));                 % should be column vectors !
N       = length(x);
s       = sum(x.^2)/(2*N);

应用举例

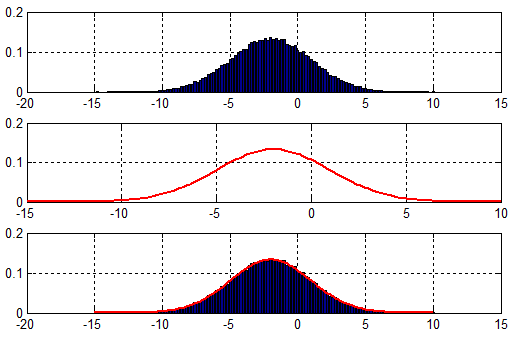
以正态分布为例：

rng('default') % for reproducibility
x = 3*randn(100000,1)-2;
%fitting
x       = x( : );                 % should be column vectors !
N       = length(x);
u       = sum(x)/N;
sig2    = (x-u)'*(x-u)/N;

%Plot

figure;
%Bar
subplot 311
numter = [-15:.2:10];
[histFreq, histXout] = hist(x, numter);
binWidth = histXout(2)-histXout(1);
bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on;
%Fitting plot
subplot 312
y = 1/sqrt(2*pi*sig2)*exp(-(numter-u).^2/2/sig2);
plot(numter,y,'r','linewidth',2);grid on;

%Fitting result
subplot 313
bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on;
plot(numter,y,'r','linewidth',2);

结果图：