常规波束形成

波束形成是阵列信号处理算法中最为基础也是应用最为广泛的一种算法，如今依旧是水声方面信号处理的主要组成部分之一。波束形成算法的功能大致可以分为两个方面，一方面是为了获得较为理想的输出信噪比，另一方面是为了获得较高的DOA分辨能力。

对于平面波而言，由于其幅度相同，所以到达基阵上的信号可以视为同一信号，但是由于各个阵元空间位置不同，导致对于同一时间接收到的信号，相对于参考阵元，各个阵元会有不同的到达时间延迟。如果采取方法对每个阵元的时延量进行补偿，再将各个阵元上的延迟信号求和，会形成一个标量输出，其目的就是形成这样一个波束，并将其扫描到一个特定的方向上。

对于由$N$个间距为$d$，特性相同的传感器组成的均匀线列阵，如果信号的入射角度和阵列的法线方向的夹角为$\theta$，则每两个相邻的传感器收到的信号时间延迟为

$\tau { \rm { = } } \frac { \lambda } { c } d\sin \theta = \frac { { 2\pi } } { w } d\sin \theta$

式中，$c$为波速，$\lambda$为波长。
以第一个阵元为参考阵元，那么为了补偿各阵元时延，以形成一个主瓣，所以常规波束形成器的加权向量可以构造为

$w(\theta ) = { [1{\rm { } } { e^ { - jw\tau } } { \rm { } } \cdots { \rm { } } { e^ { - jw(N - 1)\tau } } ] ^T }$

则该算法的波束形成器输出可以表示为

$y(t) = { w^H } (\theta )X(t) = \sum\limits_ { i = 1 } ^N { { w_i } { x_i } (t) }$ $R = E[X { X^H } ]$

实际中接收的信号都是由快拍数构成的，且因受到接收时间的限制，实际阵列接收到的数据长度都是有限的，所以无法获取理论分析所得协方差矩阵，因此只能用最大似然估计法对理论上的数值求取估计矩阵，估计矩阵表示如下：

$\hat R = \frac { 1 } { L } X { X^H }$

如果令加权向量中的观测范围可以变化，则其在形式上等同于扫描向量$a(\theta )$，则其输出功率可以表示为

${ P_ { CBF } } (\theta ) = { w^H } (\theta )\hat Rw(\theta )$

为了验证常规波束形成的方位估计效果，假设由16个各向同性的阵元组成的均匀线列阵，定义阵列的法线方向为${0^ \circ }$，阵元间距为$\lambda /2$，两个等强度的窄带信号入射到该阵列，信号的频率为2000Hz，噪声背景为高斯白噪声，同时信号和噪声不相关，快拍数为1024，改变信号的入射角度和信噪比，仿真结果如下：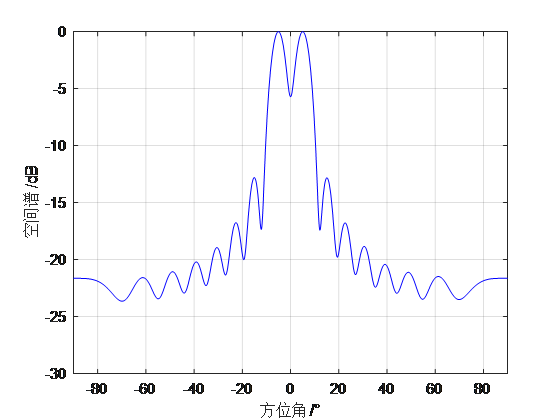

角度(-5,5),sinr=15dB

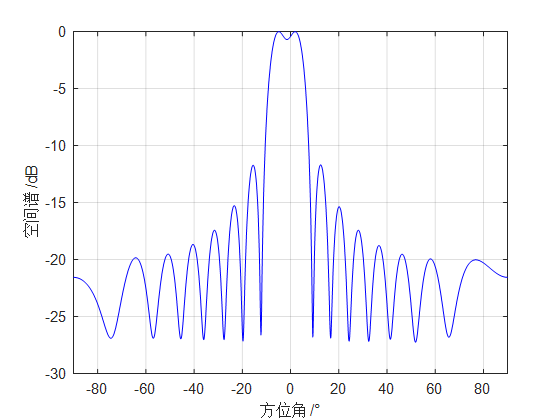
角度(-5,2),sinr=15dB

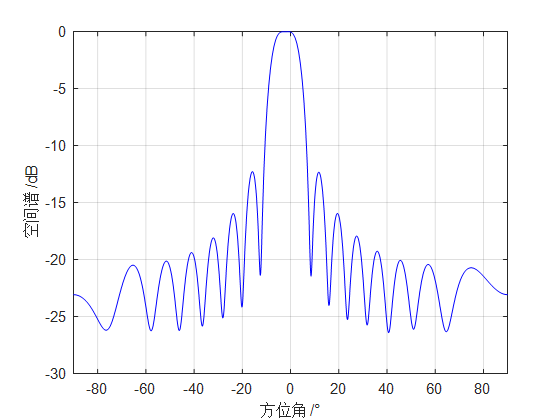
角度(-5,1),sinr=15dB

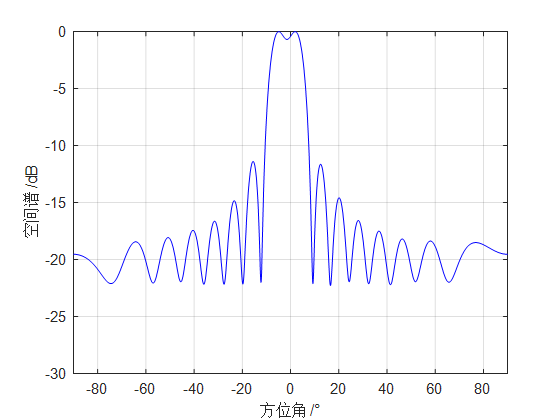
角度(-5,2),sinr=10dB

在不同信号参数下，由常规波束形成法得到的空间方位谱分别在图(a)、(b)、(c)、(d)给出。当两个信号的入射角间隔${6^ \circ }$，信噪比为15dB时，如图(c)所示，已经无法正常分辨两个目标，保持信噪比不变，增大信号入射角度间隔至${7^ \circ }$，如图(b)，已经能够分辨两个目标，并且能给出目标正确的入射方向，如将间距增大到${10^ \circ }$，则图(a)，两个信号已经完全分离，在各自来波方向均有明显的峰，在将入射角度间距设置在${7^ \circ }$的情况下，令信噪比SNR下降至10dB，从图(d)中可以看到，由于入射的信号能量较低，输出数据的信噪比明显降低。

参考文献

Worsley K J, Evans A C, Marrett S, et al. A three-dimensional statistical analysis for CBF activation studies in human brain[J]. Journal of Cerebral Blood Flow & Metabolism Official Journal of the International Society of Cerebral Blood Flow & Metabolism, 1992, 12(6):900-18.
孙超. 水下多传感器阵列信号处理[M]. 2007.