关于工程对点
SVD性质
关于SVD定义,计算,请参考[1]。
对于奇异值,它与特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的下降特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
即也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵:
其中k比𝑛小很多(m>n>k),也就是一个大的矩阵𝐴可以用三个小的矩阵 𝑈𝑚×𝑘 Σ𝑘×𝑘 𝑉𝑘×𝑛𝑇来表示。如下图所示,现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了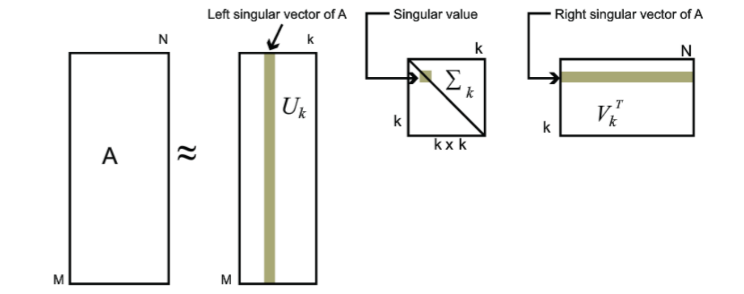
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。同时,介绍这个性质在后面解决符号模糊问题中有重要应用。
符号随机性问题介绍
利用上面推出的SVD性质,即:
改写成如下向量形式:
对每一组奇异向量满足如下:
这样SVD分解本身不提供计算每个特征向量符号的方法。在实际算法实现时,这种不确定性是继承的,因此单个奇异向量有一个“任意”符号。这个符号是计算分解稳定数据时的副产品,所以确定的符号跟随机分配没有区别,因此,就分解所代表的数据而言,符号没有任何意义的解释。
符号随机性影响
正数数值影响
虽然上面的问题在数学上没有任何影响,但是在实际应用中有非常大的影响。
下列数据表格为不同国家,三种酒的平均消费量每年,人均预期寿命,心脏病发病率,具体如下: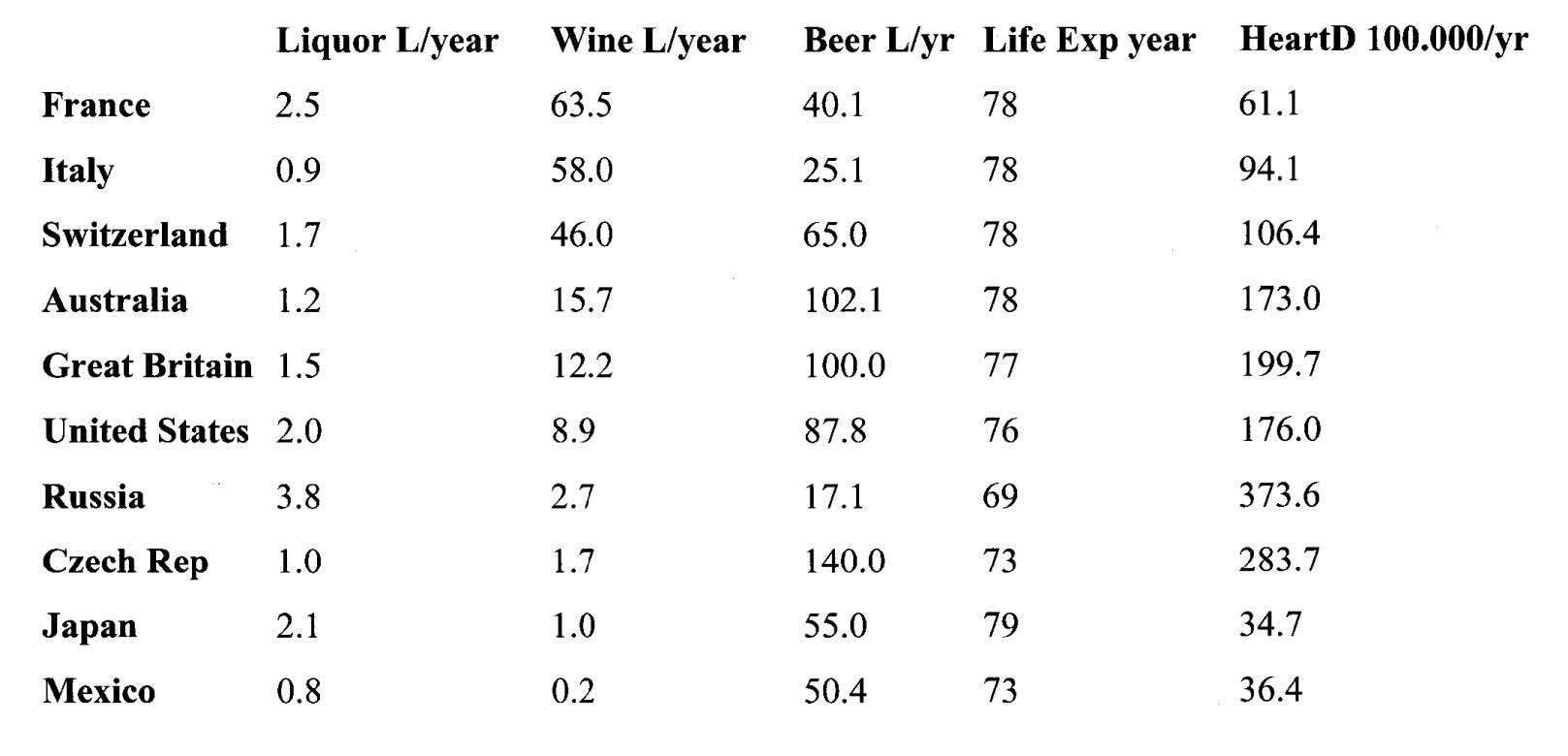
A矩阵和Matlab结果如下:
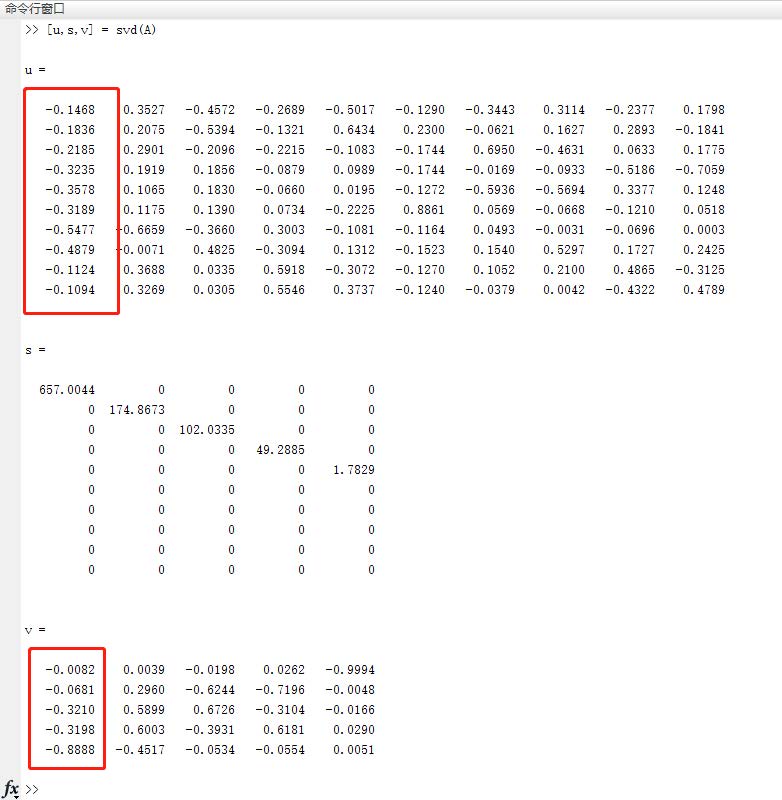
尽管A是很明显的正数数据,但是奇异向量仍然全部是负号。事实上,现在matlab 使用的线性代数包对 SVD 的实现,来自全正矩阵的第一个奇异向量总是有全负的元素。
音频影响
在音频数据处理中,比如使用MVDR做如下对比实验:
- 正常使用 Matlab中SVD函数结果生成音频。
- 将SVD结果符号全部翻转生成音频。
- 随机翻转SVD结果符号生成音频。
1/2对比: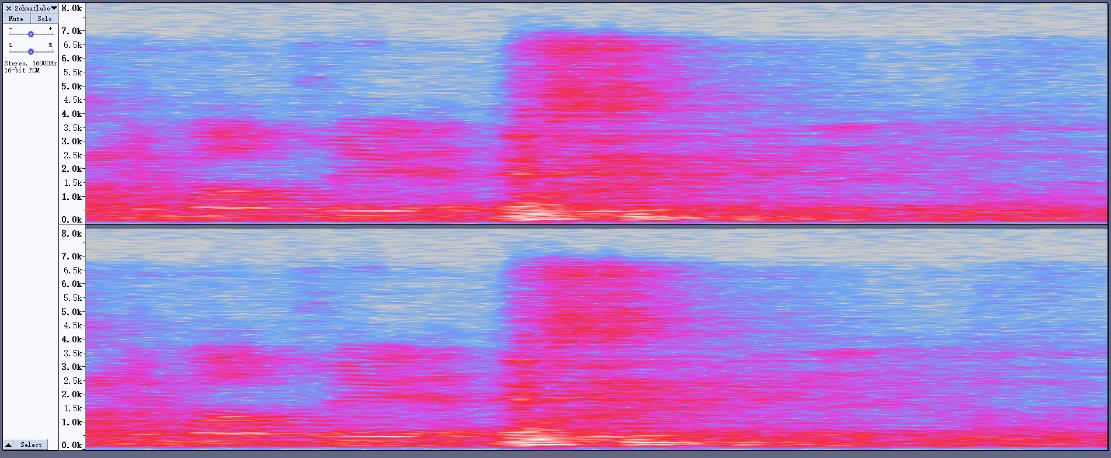
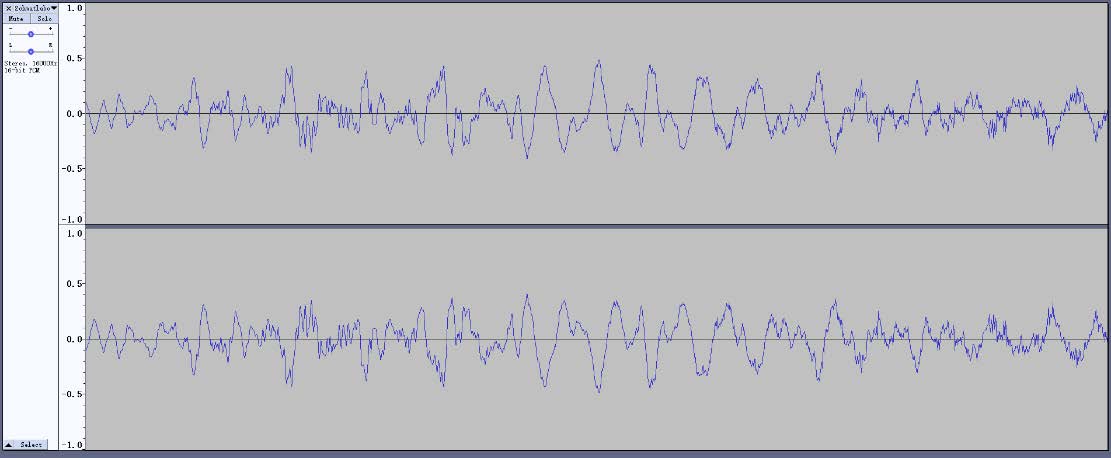
1/3对比: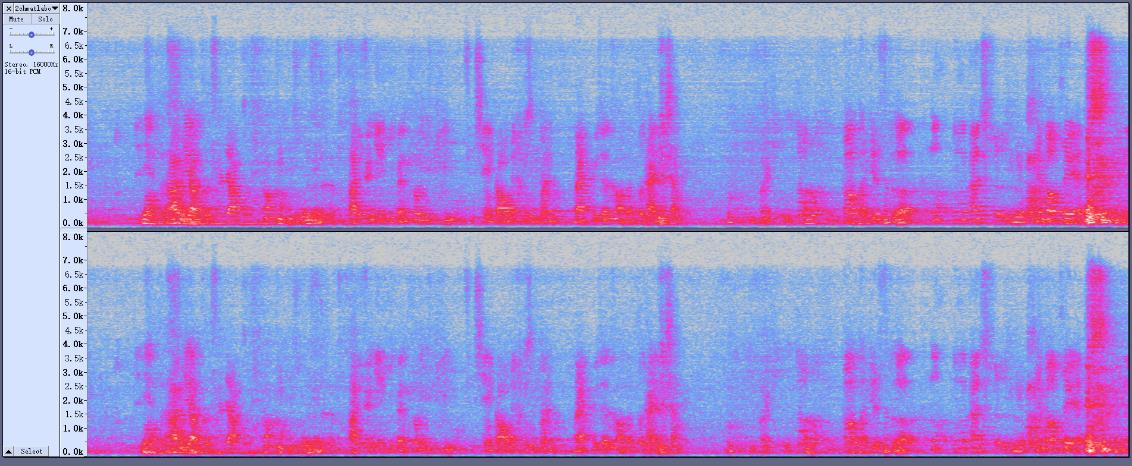
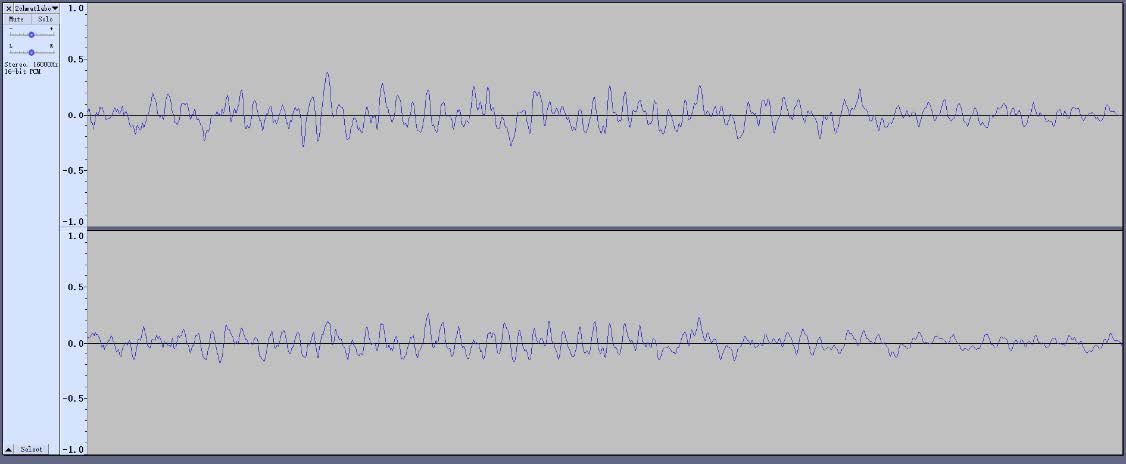
从数学的角度是没有办法避免成对奇异向量乘法项符号的不确定性。因此数学不能指导做符号选择。但是,数据分析不仅仅只能用代数。为了确认奇异向量的符号,建议它与所表示的其他大部分向量的方向相同。从几何学上解释,向量应该指向相同的方向,而不是相反的。解决方法介绍
举个例子:下图为二维数据的一些例子和相应的第一个右奇异向量和修正后的向量。普通细线为所表示的多数向量,粗虚线是SVD后的第一右奇异向量,粗实线是矫正后的向量。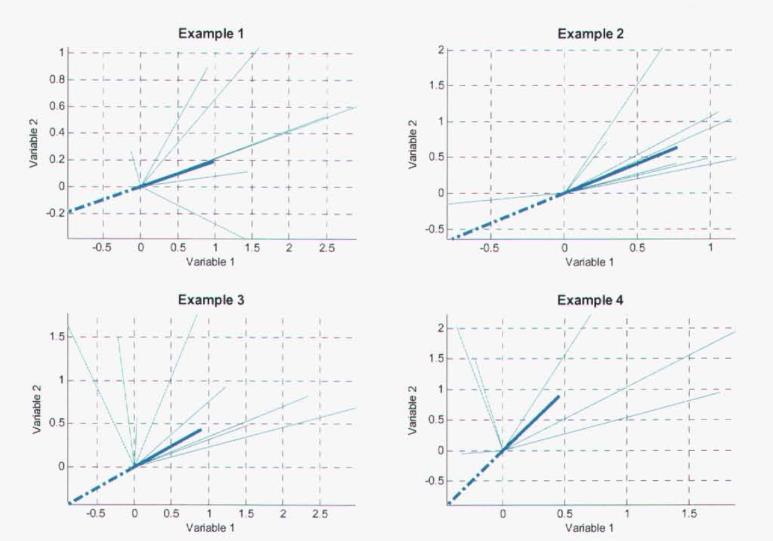
奇异向量符号确定算法
确定符号可以由奇异向量和单个独立数据的内积符号确定。单个数据向量可能会有不同的方向,但是选择大多数向量的方向是比较直观和实用的。这可以通过计算有符号内积的和的符号来找到。
举个例子,我们希望确定第k个左奇异向量符号。
理想的情况下如果奇异向量同数据列向量有正确的符号关系,我们有如下关系:实际情况下,我们选择最大的符号:如果用这种方法计算左右奇异向量的两个最优符号不一致,则可以通过选择左右奇异向量绝对值最高的符号来确定整体符号。算法步骤
输入:数据矩阵、待确定符号的第k个左右奇异向量
输出:矫正符号后的左右奇异向量 - 求左奇异向量符号
- 求右奇异向量符号
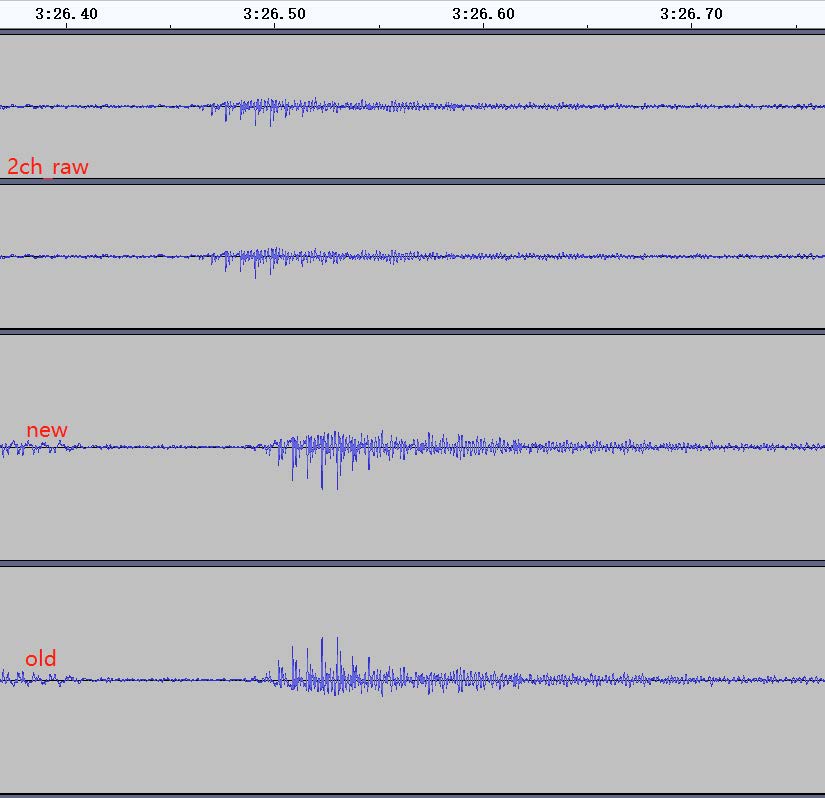
- 确定符号使用该方法将MVDR中的SVD结果进行校验,音频对比结果如下:
1
2
3
4
5
6
7
8
9
10
11if ((s_left)*(s_right))<0
{
if(abs(s_left)<abs(s_right))
{
s_left = -(s_left);
}
else
{
s_right = -(s_right);
}
}
实践及结论
Matlab 中使用的 LAPACK Linear Algebra PACKage求解 SVD 方法会按照它内置的逻辑将奇异向量的方向尽可能的统一( 测试音频中有 86.75% 是一致的,整体符号相反),但是可能出现整体相反的情况。
符号模糊问题解决算法的意义:
- 可以从将SVD的输出进行校验,方法可以跨平台移植,任何平台上,不同实现方法的 SVD通过该方法,都可以获得接近100%一致的方向性。优化版本的SVD函数可以在项目中使用。
- 虽然音频质量可能没有质的飞越,但是波形相位得到校正,SVD方向准确率提升一定百分比,使用数学方法带来的不确定性问题得到严谨的解释和解决。
参考文献
[1] 博客
[2] 线性代数及其应用.第三版 David C.Lay 著