空域矩阵预滤波DOA估计

实际阵列在接收信号的同时，由于复杂的环境影响，往往会伴有很多干扰信号，但是只有一部分方位是人们感兴趣的，所以对其他方位的噪声以及干扰进行抑制是非常有必要的，由此需要一个空域滤波器，能够做到只让来自感兴趣方向的信号通过，并且抑制来自其余不感兴趣方向的信号。

矩阵空域滤波器以及波束域滤波器是空域滤波器中最为主要的两大分支。其中矩阵空域滤波器是比波束域滤波器更为合适作为预滤波器的一种空域滤波器，该滤波器不仅有着空域滤波器的基本特性，最为重要的一个特性就是，该滤波器处理完阵列信号后输出的数据不同于波束域滤波器输出的波束域信号，其输出仍为阵列信号。因此可以改良阵列数据，进而达到预处理的目的以及达到提高目标方位估计分辨率以及目标检测的能力。

空域矩阵滤波器原理

由阵列信号模型，对于一个由N个阵元构成的任意阵列，自远场入射D个窄带信号，方向角为${\Theta _D} = [{\theta _1}, \cdots {\theta _2} \cdots {\theta _D}]$，假设各个信号之间互不相关，则接收到的数据可以表示为如下形式：

$$x(t)=A\left(\Theta_{D}\right) s(t)+n(t)$$

引入一个$N \times N$的矩阵$G$，作为滤波器对阵列接收信号进行滤波，则经过预处理的信号输出可以表示为：

$$\begin{aligned} y(t) &=G^{H} x(t)=G^{H} A\left(\Theta_{D}\right) s(t)+G^{H} n(t) \\ &=C\left(\Theta_{D}\right) s(t)+n_{c}(t) \end{aligned}$$

其中$C({\Theta _D}) = {G^H}A({\Theta _D})$，可以等效为空域滤波后的阵列流形，${n_c}(t) = {G^H}n(t)$为原数据经过滤波的噪声数据矩阵。
为了使矩阵滤波器具有空域滤波的特性，使空域滤波后的阵列流形需要能抑制不感兴趣方位的信号，同时可以允许感兴趣方位的信号能无失真的通过，则需要满足如下约束条件：

$$G^{H} a(\theta)=\left\{\begin{array}{cl} a(\theta), & \theta \in \Theta_{P} \\ 0, & \theta \in \Theta_{s} \end{array}\right.$$

其中${\Theta _P}$表示感兴趣的扇面方位角，包含有希望处理的信息，称为通带扇面，${\Theta _S}$表示需要对信号进行抑制的扇面方位角，称为阻带扇面。

阻带约束通带最小均方准则

基于阻带约束通带最小均方准则设计的空域矩阵滤波器优化问题可以表示为：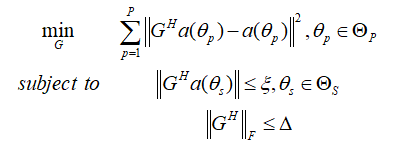

其中$\xi $表示阻带扇面内的噪声衰减率，不等式约束$\left|G^{H}\right|_{F} \leq \Delta$是限制滤波后的噪声功率在一定范围内。
为了将此优化问题转化为二阶锥规划问题，构建一个新的约束不等式:

$$\left\|G^{H} a\left(\theta_{p}\right)-a\left(\theta_{p}\right)\right\|^{2} \leq \varepsilon, p=1,2, \cdots, P$$

其中$\xi $为一个非负变量，则上述优化问题可以用下列方式表示：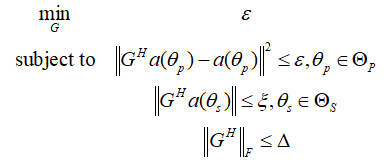

将滤波矩阵$G$按行分为N个行向量，则${G^T} = [{g_1},{g_2}, \cdots {g_N}]$，所以$G = [g_1^T,g_2^T, \cdots g_N^T]$。定义$y = {[\varepsilon ,{g^T}]^T}$，$b = {[1,{0_{1 \times {N^2}}}]^T}$，同时满足$\varepsilon {\rm{ = }}{b^T}y$，则：

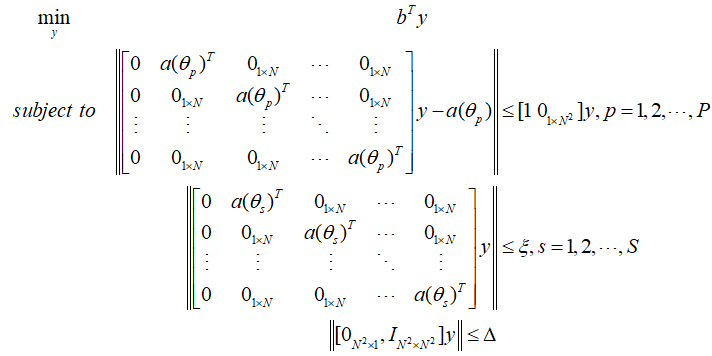
由此将阻带约束通带最小均方优化问题转变为标准的二阶锥规划形式，可以求得$y$的最优解，以其第$2 \sim\left(N^{2}+1\right)$个元素，重组得到$N \times N$维的滤波矩阵$G$。

空域矩阵预滤波DOA估计与仿真分析

MUSIC算法属于目标方位估计的经典算法之一，相比于常规波束形成等算法，具有更高的分辨率，但是MUSIC算法在低信噪比、或者小快拍等情况下，性能会大幅下降。当阵列接受到目标信号后，通过空域矩阵滤波器对数据进行加工处理，在不影响通带扇面信号的情况下抑制阻带扇面内的干扰以及噪声。空域矩阵滤波器相对于其他的阵列信号预处理算法的一个明显优势是滤波器的输出数据仍为阵元域数据，经过此方法处理的数据仍可以被很多阵列信号处理算法应用，以达到抑制空间某方向干扰的目的。本节将预滤波的信号采用MUSIC方法进行方位估计，同时与经典MUSIC算法对比，分析包括分辨率、信噪比门限等在内的性能指标。

空域矩阵预滤波DOA估计基本原理

经过空域滤波的信号协方差矩阵为：

$${R_y} = E[y{y^H}] = C(\Theta ){R_S}{C^H}(\Theta ) + {R_c}$$

其中阵列接收信号协方差矩阵${R_s} = E[s{s^H}]$，滤波后的噪声协方差矩阵${R_c} = {G^H}E[n{n^H}]G$。根据上式，采用MUSIC算法对滤波后的数据进行DOA估计，对滤波数据协方差矩阵${R_y}$进行特征分解，

$${R_y} = E\Lambda {E^H}$$

其中 ，$\Lambda=\left[\begin{array}{cc}\Lambda_{S} & 0 \ 0 & \Lambda_{N}\end{array}\right]$为特征值矩阵，${\Lambda _S}$为较大的$D$个特征值，${\Lambda _N}$为较小的$N - D$个特征值，$E=\left[\begin{array}{ll}E_{C S} & E_{C N}\end{array}\right]$为特征向量组成的矩阵，${E_{CS}}$以及${E_{CN}}$分别是${\Lambda _S}$和${\Lambda _N}$对应的预处理后的特征向量张成的信号子空间与噪声子空间。

由此方法生成的空域矩阵滤波器通带响应与期望响应仍然会存在一定误差，即经滤波处理后的信号会发生一定程度的畸变，为了消除该误差的影响，需要对MUSIC算法的方位谱表达式做调整，则基于矩阵预滤波的MUSIC空间谱的峰值位置表达式为：

$$P_{P-\text { Masic }}(\theta)=\frac{c^{H}(\theta) c(\theta)}{c^{H}(\theta) E_{C N} E_{C N} c(\theta)}, \theta \in \Theta$$

其中$c(\theta ) = {G^H}a(\theta )$为接收信号滤波后等效的阵列流形矢量。

仿真分析

对于一个由16个各向同性的阵元构成的均匀线列阵，三个等强度的非相干窄带信号源自远场分别由${\rm{ - }}{5^ \circ }$，${5^ \circ }$，${50^ \circ }$三个方向入射到阵列，接收信号背景噪声为高斯白噪声且与信号不相关，基于阻带约束通带最小均方准则设计滤波器进行仿真分析，对接收信号的目标方位进行估计，通过MUSIC算法对信号源进行空间谱估计，并与常规的MUSIC算法处理效果进行对比，分析空域矩阵滤波器的性能。令滤波器通带扇面${\Theta _P} = [ - 15,15]$，阻带扇面${\Theta _S} = [ - 90, - 21] \cup [21,90]$，通带和阻带之间的过渡带${\Theta _T} = [ - 20, - 16] \cup [16,20]$，矩阵的Frobenius范数约束值为1.65，噪声衰减率为0.35，仿真结果如下：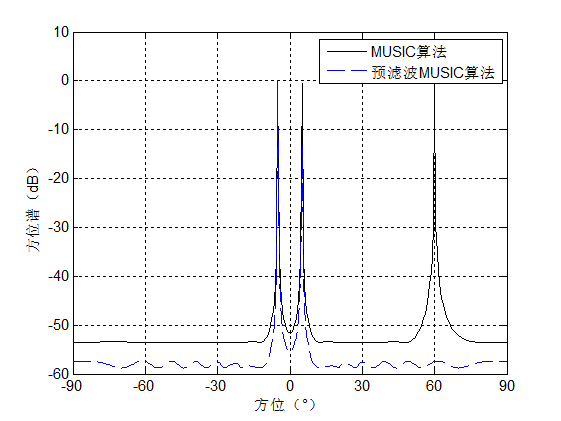

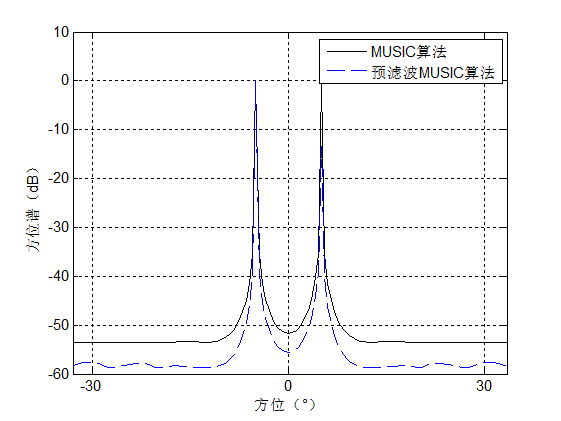
(a)预滤波算法对阻带干扰抑制效果曲线

(b)预滤波算法的方位分辨率效果曲线

从图中可以看出，无论是常规MUSIC算法或者空域矩阵预滤波MUSIC算法都可以有效正确的估计出目标的方位信息，并且预滤波MUSIC算法在阻带扇面范围抑制干扰和噪声效果明显，能够抑制来自$50^ { \circ }$方向的干扰，在通带扇面范围内的信号具有更高的分辨能力，谱峰更为尖锐，更加适合用于多个目标的方位估计。

仿真分析常规MUSIC算法以及基于空域矩阵滤波后的MUSIC算法在信噪比不同的情况下，有效估计目标方位的概率，设定信噪比为$[ - 15:1:15]$dB，每个信噪比进行100次独立实验，如果两个信号的估计方位$\widehat{\theta}_{1}$和$\widehat{\theta}_{2}$满足：

$$\left|\hat{\theta_{1}}-\theta_{1}\right|+\left|\widehat{\theta}_{2}-\theta_{2}\right|<\left|\theta_{1}-\theta_{2}\right|$$

则认为其估计有效，最终计算有效概率，仿真结果如下，

信噪比不同情况下算法估计有效概率曲线

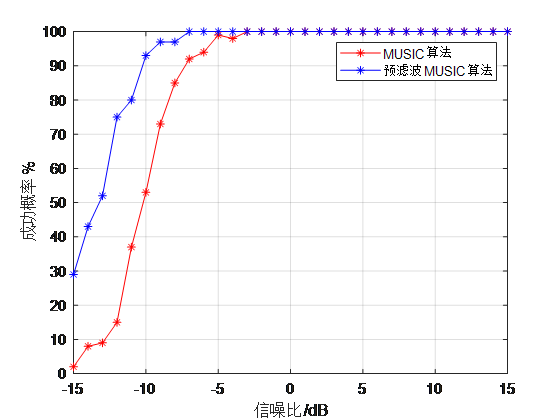
图中显示了不同信噪比下两种方位估计算法的有效分辨概率，可以看出，空域矩阵滤波MUSIC算法具有更低的信噪比门限，在-15dB时，常规MUSIC算法几乎已经无法估计目标方位，但预滤波MUSIC算法已经可以在30%以上的概率可以有效估计目标，在信噪比高于-5dB时，两种方法均能正确估计目标方位，可见在低信噪比时预滤波MUSIC算法目标方位分辨能力明显优于常规MUSIC算法。

(a)信噪比不同情况下的估计误差曲线

(b)信噪比不同情况下的估计标准差曲线

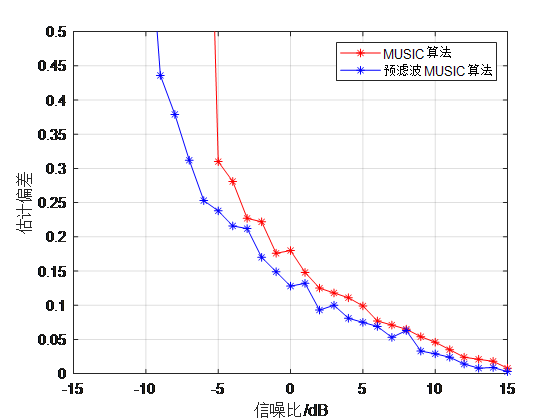
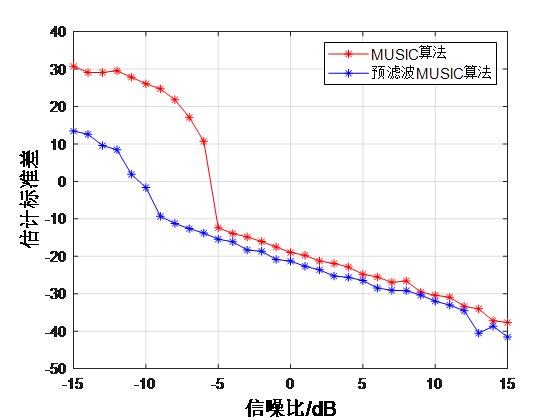
从图(a)、(b)中可以看出，当信噪比比较低时，预滤波MUSIC算法的估计偏差以及标准差明显低于MUSIC算法，随着信噪比的提高，差别越来越小。
由以上的仿真分析，该矩阵滤波器对阻带扇面内的噪声和干扰具有明显的抑制作用，提高了滤波器通带扇面内信号的方位分辨率，并且可以降低基于空域矩阵滤波方位估计时所使用算法的信噪比门限。

参考文献

1. Kobayashi K, Kim S, Kojima M. Correlative Sparsity in Primal-Dual Interior-Point Methods for LP, SDP, and SOCP (ENG)[J]. Applied Mathematics & Optimization, 2008, 58(1):69-88.
2. Sturm J F. Using SeDuMi 1.02, A Matlab toolbox for optimization over symmetric cones[J]. Optimization Methods & Software, 1999, 11(1-4):625-653.
3. Nesterov. Introductory Lectures on Convex Optimization: A Basic Course
4. 冯杰, 杨益新, 孙超. 自适应空域矩阵滤波器设计和目标方位估计[J]. 系统仿真学报, 2007, 19(20).